発達経過記録から、総合的な発達のバラツキを示す指標を試作

発達指数の試み
保育所保育において、とても重要な記録である、発達経過記録を匿名データ化し、分析することを続けている。その中で、子どもたちの発達度合を印象づける要因、すなわち発達のバラツキを感じさせる「保育の内容」領域が、どこになるかということが課題になってきた。
これまでの多数のクラスの主成分分析結果の確認から、主成分分析の結果である第1成分が、数十に渡る発達記録項目の情報を圧縮した、いわば総合的な発達度合、状況を示すものになるのではないかと気がついた。
そこで、第1成分の結果数値を、最大限利用することで、発達経過記録から、総合発達指数のようなものを概念できるのではないかと考えてみたところだ。
要すれば、第1成分の因子(主成分)負荷量を指数化する上でのウェイトとすることで、「総合的に」発達のバラツキを示す一次元のスカラー量化、つまり、指数化することを試みてみたということだ。
指数の計算方法
まず、指数化のためには、ウェイトが必要となるが、そのウェイトとして、主成分分析の第1成分における因子(成分)負荷量を採用した。その主成分分析は、個々の発達記録項目のスコアではなく、それらの発達記録項目を、保育指針における「保育の内容」の領域分割(ただし、領域「健康」については、運動機能と生活習慣に分割)ごとに平均値を計算し、この数値をもって主成分を計算することとした。
その主成分分析の結果となる第1成分は、寄与率で90%近いものとなっており、データのバラツキを相当程度説明できるものであった。この第1成分の各領域のスコアに対する負荷量をウェイトとする加重平均を施し、指数化してみた。
総合指数の配置状況
この総合指数の対象(インスタンス)の配置状況を可視化してみた。具体的な描画は次のようにしている。
- インスタンスをスコア順にソートしてナンバリング
- ナンバリング順に横軸にインスタンスを配置
- 縦軸は、対応するスコア値
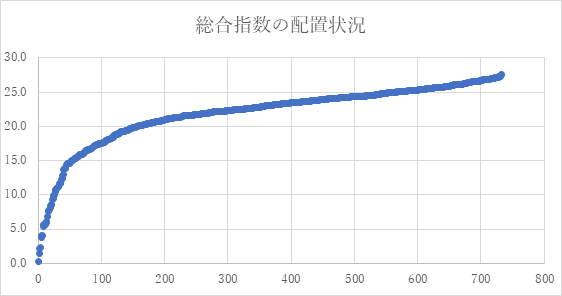
このような配置状況は、どのような数式で、近似できるであろうか?
まず、直観的に可能性に気づくのは、対数関数である。下に対数関数のグラフを掲げる。
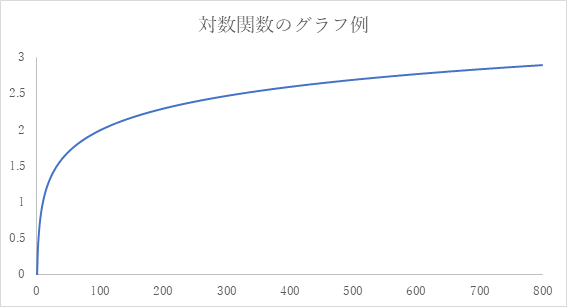
総合発達指数のランキングの配置状況が、このような対数関数のグラフで近似できるということであれば、左端のランキングの低い部分(上図では、概ねスコア100以下の部分)では、子どもの存在数が疏(まばら)になっており、徐々に子どもの存在数が増えていくという「度数分布」になっていると考えられる。
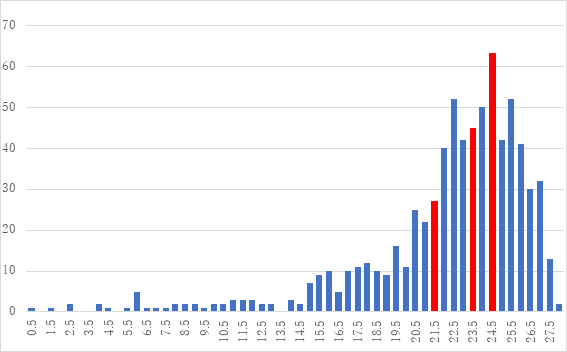
実際の度数分布
そこで実際に度数分布、ヒストグラムを確認してみると、下のように、左に裾の長い分布になる。平均値は21.9、中央値は23.5、そして最頻値は24の区分となっており、平均値は、下に大きく歪んでいるようだ。園児数約700に対し、平均以上の指数値の園児数が500を超えていた。この点では、対数関数グラフの左端部分の示唆する度数分布と整合的だ。しかし、ヒストグラムでは、右端にダウンスロープが生じており、これは対数関数での近似と整合しない。
シグモイド関数
改めて、総合指数ランキングの配置状況を確認すると、右端に少しせり上がっている部分がある。この部分が、対数関数のグラフに当てはまらない部分となる。そこで、どのような関数が当てはまるか探索してみると、シグモイド関数が当てはまるのではないかと考えられる。
下記のグラフは、一般的なシグモイド関数の横軸と縦軸を反転(逆関数)させ、その描画域を、指数の値域に合わせて、制限したものである。
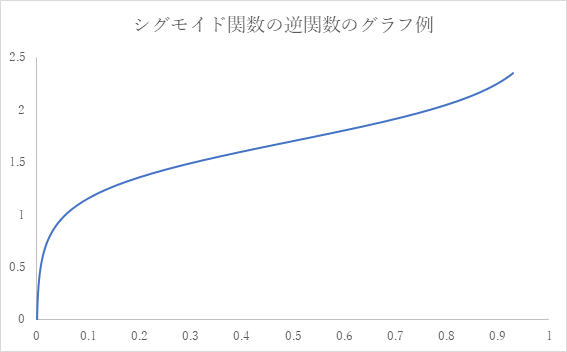
上の度数分布を確率密度関数の近似と想定できれば、このシグモイド関数(の逆関数)が、総合発達指数の累積密度関数ということができることになる。勿論、この場合のこの分布は、事象の範囲に上限と下限があるものなので、扱いが難しい部分はある。
いずれにせよ、グラフの線が水平方向になだらか、滑らかな部分では、インスタンスの人数の増加度合が高くなり、垂直方向により近くなっている部分では、インスタンスの増加程度が低くなっていること示している。
正規分布に従う「指数」の意味
ある種のシグモイド関数を微分したもののグラフは正規分布の形状になることが知られており、それは、正規分布の累積密度関数が、シグモイド関数のタイプに属する関数であることを示している。
これを踏まえると、今回試作した総合発達指数は、正規分布に従うということなのかも知れない。これは、先に紹介したヒストグラムが、正規分布のグラフ(の一部を切り出したもの)のように見えたことからも、実は想像できた事なのかも知れない。
なお、若干、右側の裾の膨らみが、左側に比べて「膨らんでいる」ように見えるのは、この指数の基礎データの値には、上限があり、その上限に多くの子どものデータが貼り付いているため、いわば正規分布に比べて、少し裾の広がりが圧縮されていることの結果ではないかと思われる。
さらに話しを遡らせれば、中心極限定理から、正規分布に従う確率変数は、多くの確率変数の平均と解釈できるので、今回の総合発達指数にも同様のことが当てはまる。確かに、確か位に、この指数は、数十項目の行動の達成時期のスコアを加重平均したものなので、この「多数の要素」の平均という性質を持っている。
「発達」という現象の本質がなんなのかということについて私自身は、モヤモヤした感じを持っており、「人は発達として何を見ているのか」という問題についての探求は続けていたいと思っている。そのような状況の下で、確率変数の平均値という統計量によって、発達の度合を示す指標が構成されるという可能性を見出したことから、その統計的構成物としての解釈の可能性が示されたと思っている。
つまり、今回の指数の試作によって、「多数の要素の合計、合算」としての「発達」という視角、視点、つまり、「発達」という「1つの本質的現象」があるのではなく、多くの独立した現象の構成体が「発達」というカテゴリーであるということの数学的表現の可能性ということである。
指数を試作してみたことによって、この指数の実在性について思いが及び、「発達」概念の実在論/唯名論の考えを一歩進めることができたような気がするが、この点については、更に思考過程を整理してから、別の機会に論じることにしたい。
<関連記事>
